Short article - I was thinking you could apply convolution to solve the Game of Life logic. So I quickly built a class to do just that:

class GameOfLife:
    def __init__(self, shape=(3, 3)):
        self.shape = shape
        self.state = np.zeros(self.shape, dtype=int)
        # kernel to sum neighbours
        self.kernel = np.ones((3, 3), dtype=int)
        self.kernel[1, 1] = 0

    def update_state(self):
        # convolve kernel and apply game of life logic to number of neighbours
        conv_state = scipy.signal.convolve2d(
            self.state, self.kernel, mode="same"
        )
        temp_state = np.zeros(shape=self.shape)
        temp_state[(conv_state < 2) | (conv_state > 3)] = 0
        temp_state[
            ((conv_state == 2) | (conv_state == 3)) & (self.state == 1)
        ] = 1
        temp_state[conv_state == 3] = 1
        self.state = temp_state

    def random_starting_grid(self, density=0.1):
        self.state = np.random.rand(self.shape[0], self.shape[1]) < density

    def plot_state(self):
        return plt.imshow(self.state)

    def _animate(self, _):
        self.update_state()
        self.ax.clear()
        self.ax.imshow(self.state)
        self.ax.set(xticklabels=[], yticklabels=[])
        self.ax.tick_params(bottom=False, left=False)

    def animate(self, filename):
        self.fig, self.ax = plt.subplots(figsize=(12, 12), dpi=self.shape[0])
        ani = animation.FuncAnimation(
            self.fig, self._animate, frames=300, interval=10
        )
        ani.save(filename)
        return ani

It works well. With larger sized grids we could utilise fast Fourier transforms to compute the convolution using multiplication instead.

To try to out:

game = GameOfLife(shape=(30, 30))
np.random.seed(42)
game.random_starting_grid(density=0.2)
game.plot_state()
game.animate("vid.gif")

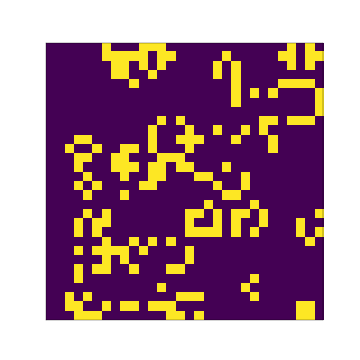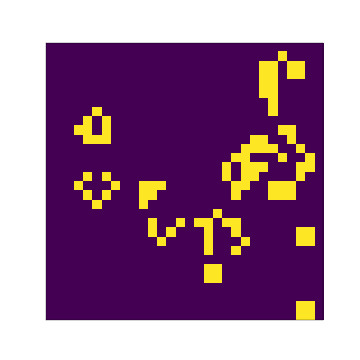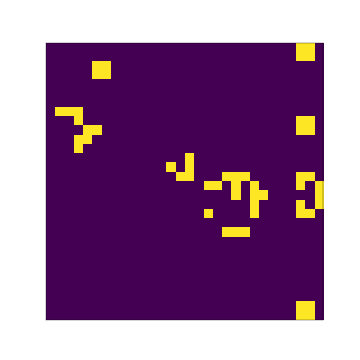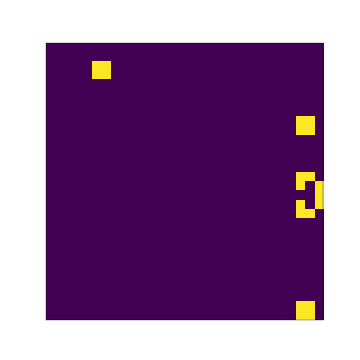
You can try larger grid sizes as well:

game = GameOfLife(shape=(200, 200))
np.random.seed(42)
game.random_starting_grid(density=0.2)
game.plot_state()
game.animate("vid_large.gif")

Full code available here:
https://github.com/stanton119/data-analysis/tree/master/other/game_of_life